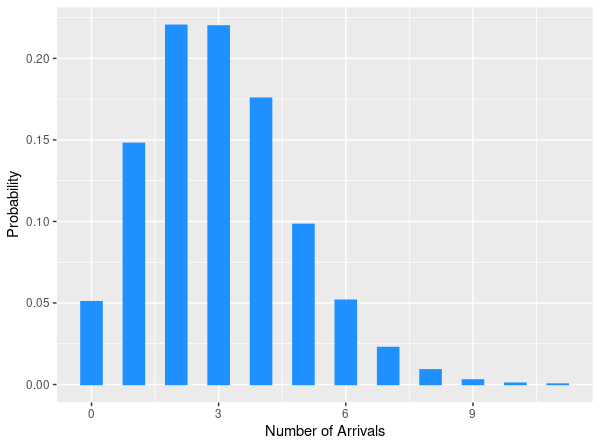
The Poisson random variable describes the probability that a given number of events occurs within a fixed time interval. It is a discrete random variable with a single parameter \(\lambda\).
Probability Mass Function
The Poisson distribution has the PMF
\[p_X(k)=\dfrac{\lambda^k}{k!}e^{-\lambda}\]where \(k=0,1,2,\ldots\)
Expectation
The mean of a Poisson random variable is
\[\mathbb{E}[X]=\lambda.\]$$\begin{align} \mathbb{E}[X]&=\sum_{k=0}^{\infty}k\frac{\lambda^k}{k!}e^{-\lambda}=e^{-\lambda}\sum_{k=1}^{\infty}\frac{\lambda^k}{(k-1)!}\\ &=e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^{k+1}}{k!}\\ &=\lambda e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^k}{k!}\\ &=\lambda e^{-\lambda}e^{\lambda}\\ &=\lambda \end{align}$$
Variance
The variance of a Poisson distribution with parameter \(\lambda\) is
\[\mathrm{var}(X)=\lambda.\]To calculate the variance, we use $$\mathrm{var}(X)=\mathbb{E}[X^2]-(\mathbb{E}[X])^2=\mathbb{E}[X(X-1)]+\mathbb{E}[X]-(\mathbb{E}[X])^2.$$ The first term is $$\begin{align} \mathbb{E}[X(X-1)]&=\sum_{k=0}^{\infty}k(k-1)\frac{\lambda^k}{k!}e^{-\lambda}\\ &=e^{-\lambda}\sum_{k=2}^{\infty}\frac{\lambda^k}{(k-2)!}\\ &=\lambda^2e^{-\lambda}\sum_{k=2}^{\infty}\frac{\lambda^{k-2}}{(k-2)!}\\ &=\lambda^2e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^k}{k!}\\ &=\lambda^2e^{-\lambda}e^{\lambda}\\ &=\lambda^2. \end{align}$$ Then, $$\mathrm{var}(X)=\lambda^2+\lambda-\lambda^2=\lambda.$$
Binomial versus Poisson Distributions
We will show that the Poisson distribution is the limit of the binomial distribution as \(n\rightarrow\infty\) and \(p\rightarrow0\) while holding \(\lambda\) constant, with \(\lambda=np\).
First, we divide the fixed time interval into \(n\) subintervals so that the probability of getting 2 or more arrivals in one subinterval is negligible. Each subinterval can be described by a Bernoulli random variable and the probability of an arrival is \(p=\frac{\lambda}{n}\). The number of arrivals for the entire time interval is then described by a binomial random variable with the PMF
\[\mathbf{P}(X=k)=\binom{n}{k}\!\left(\frac{\lambda}{n}\right)^k\!\left(1-\frac{\lambda}{n}\right)^{n-k}.\]We can rewrite this equation, rearrange the terms as
\[\frac{\lambda^k}{k!}\frac{n!}{(n-k)!\,n^k}\left(1-\frac{\lambda}{n}\right)^n\left(1-\frac{\lambda}{n}\right)^{-k}\]and take the limit as \(n\rightarrow\infty\). Note that
\[\begin{align} \frac{n!}{(n-k)!\,n^k}&=\frac{n(n-1)\cdots(n-k+1)(n-k)!}{(n-k)!\,n^k}\\ &=\frac{n(n-1)\cdots(n-k+1)}{n^k}\\ &=1\left(1-\frac{1}{n}\right)\cdots\left(1-\frac{k-1}{n}\right) \end{align}\]so that
\[\lim\limits_{n\rightarrow\infty}\frac{n!}{(n-k)!\,n^k}=1.\]We also have
\[\lim\limits_{n\rightarrow\infty}\left(1-\frac{\lambda}{n}\right)^{-k}=1.\]Lastly, from the definition of an exponential function, we have
\[\lim\limits_{n\rightarrow\infty}\left(1-\frac{\lambda}{n}\right)^n=e^{-\lambda}.\]We have shown that the Poisson distribution is the limit of the binomial distribution when the number of trials becomes infinitely large and the probability of success or arrival becomes very small, i.e.,
\[\lim\limits_{n\rightarrow\infty}\binom{n}{k}\!\left(\frac{\lambda}{n}\right)^k\!\left(1-\frac{\lambda}{n}\right)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda}.\]Monte Carlo Simulation
library(tidyverse)
# Set the parameters
p <- 0.01
n <- 300
# lambda = p*n
B <- 10000 # Number of replications
num_arrivals <- replicate(B, {
arrival <- sample(c(0,1), size = n, replace = TRUE, prob = c(1-p,p))
sum(arrival)
})
# Plot the distribution
data.frame(num_arrivals) %>%
ggplot(aes(num_arrivals, y = ..prop..)) +
geom_bar(width = 0.5, color = "dodgerblue", fill = "dodgerblue") +
labs(x="Number of Arrivals", y="Probability")