Conditioning on an Event
Conditional PMF and Expectation
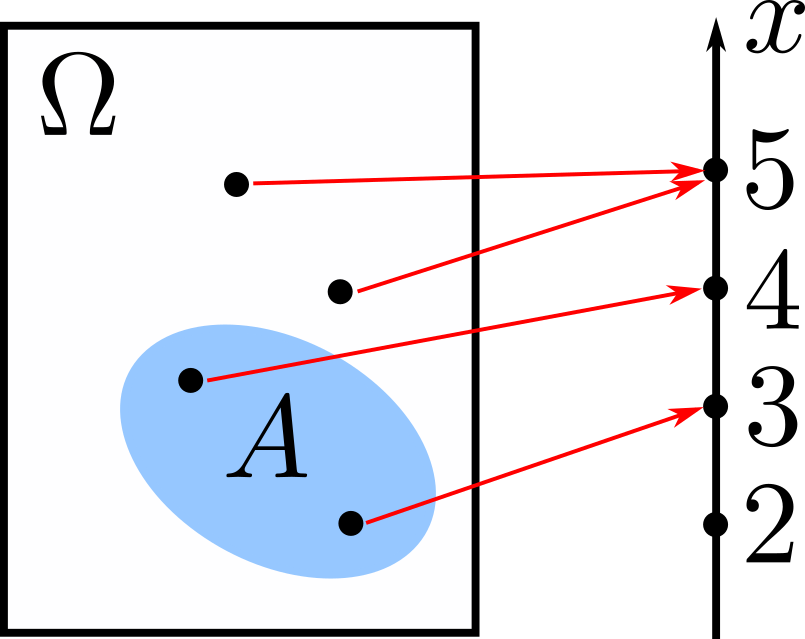
We consider conditioning on an event \(A\). Assuming that the probability that event \(A\) occurs is positive, i.e., \(\mathbf{P}(A)>0\), the conditional PMF of a random variable \(X\) given that \(A\) occurred is
\[p_{X\lvert A}(x)=\mathbf{P}(X=x\lvert A).\]Like ordinary probabilities, it is normalized, i.e.,
\[\sum_{x}p_{X\lvert A}(x)=1.\]The conditional expectation of \(X\) is then
\[\mathbb{E}[X\lvert A]=\sum_{x}xp_{X\lvert A}(x).\]Given a function of \(X\), \(g(X)\), its conditional expectation is
\[\mathbb{E}[g(X)\lvert A]=\sum_{x}g(x)p_{X\lvert A}(x).\]Total Expectation Theorem
If we divide the sample space into \(n\) disjoint events \(A_1,\ldots,A_n,\) then the expectation of \(X\) is
\[\mathbb{E}[X]=\mathbf{P}(A_1)\mathbb{E}[X\lvert A_1]+\ldots+\mathbf{P}(A_n)\mathbb{E}[X\lvert A_n].\]Conditioning on another Random Variable
We can also condition a random variable on another random variable. The conditional PMF of \(X\) given that \(Y=y\) is defined by
\[p_{X\lvert Y}(x\lvert y)=\dfrac{p_{X,Y}(x,y)}{p_Y(y)},\]assuming that \(p_Y(y)>0\). We can also condition on two random variables with the conditional PMF being
\[p_{X\lvert Y,Z}(x\lvert y,z)=\dfrac{p_{X,Y,Z}(x,y,z)}{p_{Y,Z}(y,z)}.\]Conditional Expectation
The conditional expectation of a random variable \(X\) conditioned on \(Y=y\) is
\[\mathbb{E}[X\lvert Y=y]=\sum_{x}xp_{X\lvert Y}(x\lvert y).\]Moreover, for any function \(g(X)\),
\[\mathbb{E}[g(X)\lvert Y=y]=\sum_{x}g(x)p_{X\lvert Y}(x\lvert y).\]Independence
There are several statements we can make when two random variables, \(X\) and \(Y\), are independent. First,
\[\mathbb{E}[XY]=\mathbb{E}[X]\,\mathbb{E}[Y].\]Moreover, \(g(X)\) and \(h(Y)\) are also independent, and
\[\mathbb{E}[g(X)h(Y)]=\mathbb{E}[g(x)]\,\mathbb{E}[h(Y)].\]Finally, the variance of their sum is
\[\mathrm{var}(X+Y)=\mathrm{var}(X)+\mathrm{var}(Y).\]