Definition
Suppose we want to know the probability of getting a prime number if we pick from 1 to 100. Since there are 25 prime numbers from 1 to 100, then this probability is \(\frac{25}{100}\) or \(\frac{1}{4}\). Now, suppose we are given the information that the number we pick will always be odd. Because there are 24 odd prime numbers and 50 odd numbers, then the probability of picking a prime number, given that it is odd, is \(\frac{24}{50}\) or \(\frac{12}{25}\). The probability changed because of the new information! This is called conditioning.
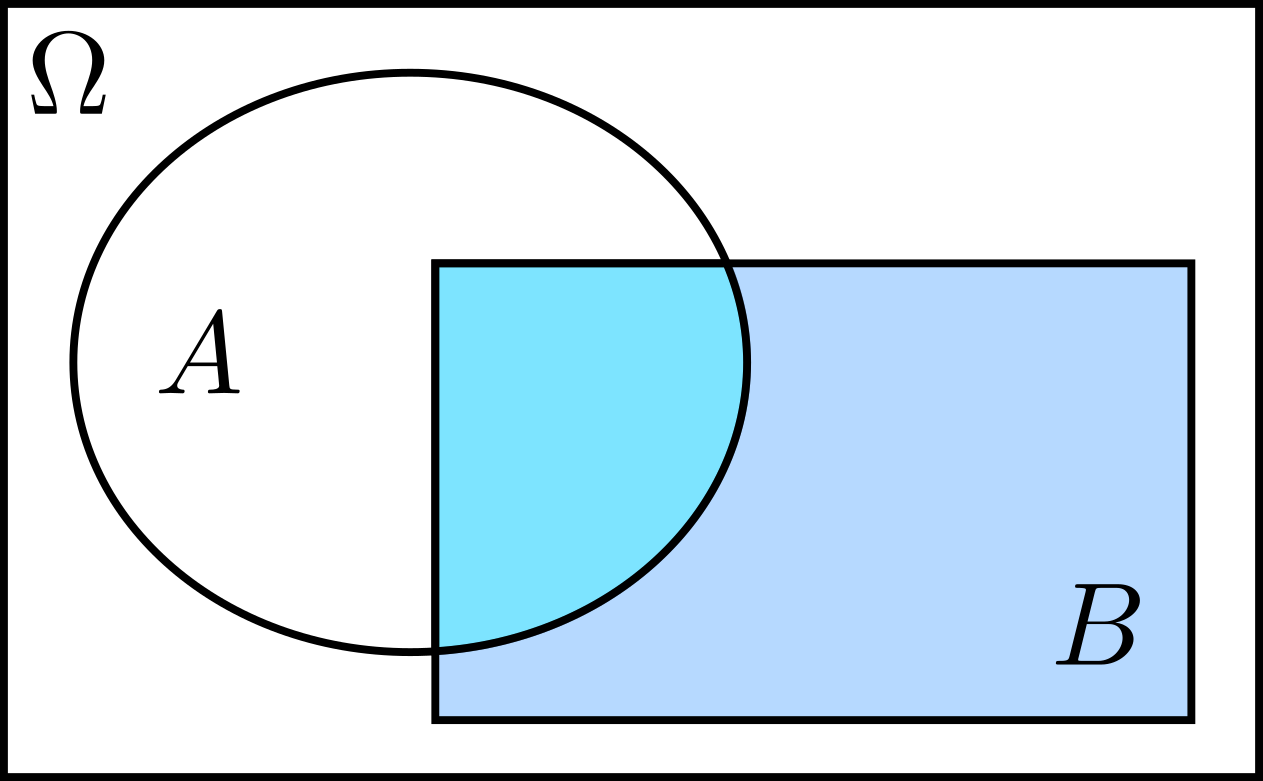
We denote the conditional probability of \(A\), given that \(B\) occurred, by \(\mathbf{P}(A\vert B)\) and it is defined as
\[\mathbf{P}(A|B)=\dfrac{\mathbf{P}(A\cap B)}{\mathbf{P}(B)},\qquad\mathbf{P}(B)>0.\]Example
We roll a 4-sided die twice. Let \(X\) be the outcome of the first roll and \(Y\) the outcome of the second roll. Moreover, let \(B\) be the event that the minimum of \(X\) and \(Y\) is 2, i.e., \(\min(X,Y)=2\). The event \(B\) is the shaded region in the figure below.
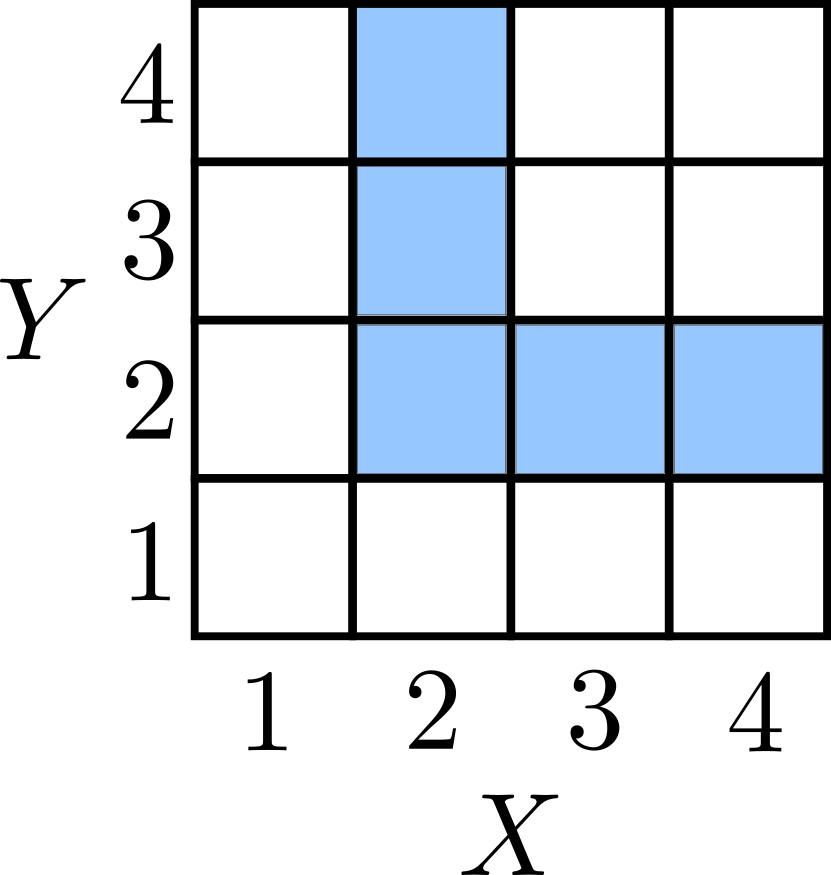
What is the probability that \(Y=1\) given that \(B\) occurred? Since \(\{Y=1\}\cap B=\varnothing\), then
\[\mathbf{P}(\{Y=1\}\,\lvert\,B)=\dfrac{\mathbf{P}(\{Y=1\}\cap B)}{\mathbf{P}(B)}=0.\]What is the probability that \(Y\) is even given that \(B\) occurred? We have
\[\mathbf{P}(\{Y=\text{even}\}\,\lvert\,B)=\dfrac{\mathbf{P}(\{Y=\text{even}\}\cap B)}{\mathbf{P}(B)}=\dfrac{\frac{4}{16}}{\frac{5}{16}}=\dfrac{4}{5}.\]Properties
Conditional probabilities share the properties of ordinary probabilities:
-
non-negativity: \(\mathbf{P}(A\lvert B)\geq0,\) assuming \(\mathbf{P}(B)>0\)
-
normalization: \(\mathbf{P}(\Omega\lvert B)=1\)
Proof: \(\mathbf{P}(\Omega\lvert B)=\dfrac{\mathbf{P}(\Omega\cap B)}{\mathbf{P}(B)}=\dfrac{\mathbf{P}(B)}{\mathbf{P}(B)}=1\)
We also have
\[\mathbf{P}(\Omega\lvert B)=\dfrac{\mathbf{P}(B\cap B)}{\mathbf{P}(B)}=\dfrac{\mathbf{P}(B)}{\mathbf{P}(B)}=1.\] -
countable additivity: If \(A\cap C=\varnothing\), then \(\mathbf{P}(A\cup C\,\lvert\,B)=\mathbf{P}(A\lvert B)+\mathbf{P}(C\lvert B).\)
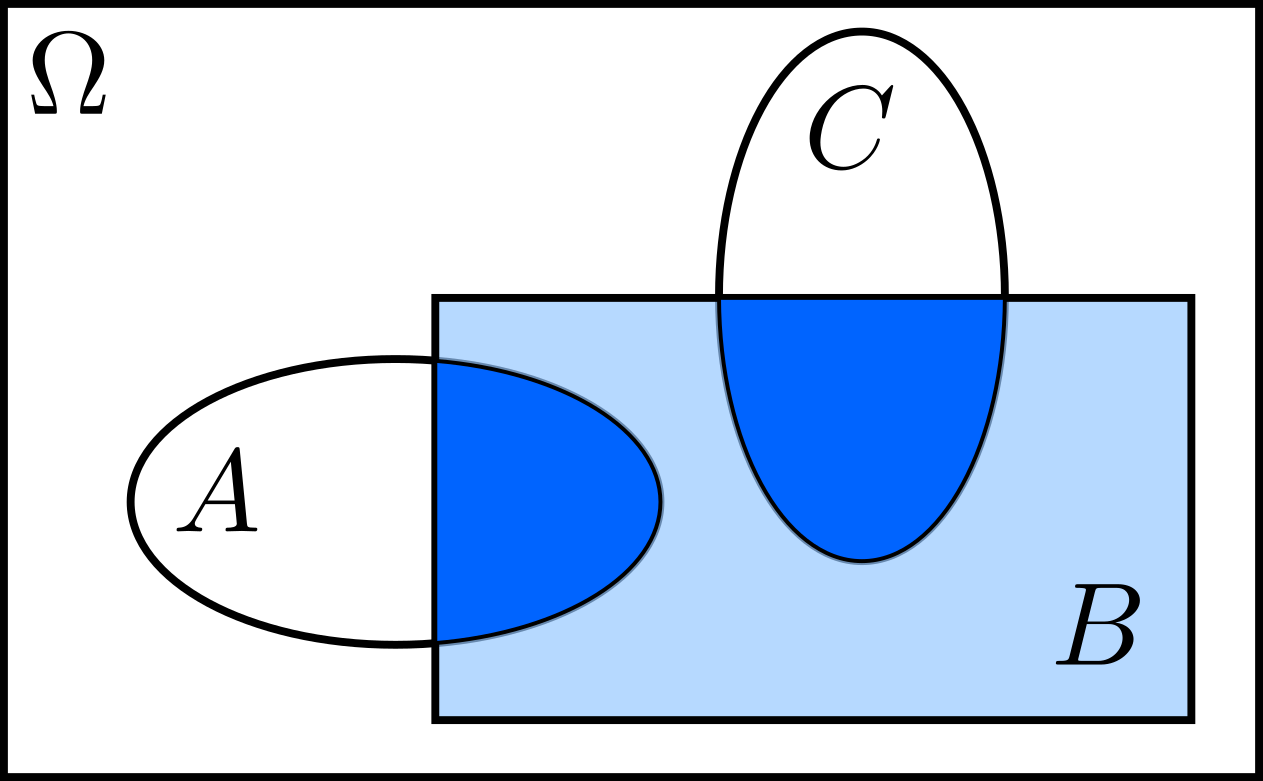
Using the figure above, we have
\[\begin{align} \mathbf{P}(A\cup C\lvert B)&=\dfrac{\mathbf{P}\left((A\cup C)\cap B\right)}{\mathbf{P}(B)}\\ &=\dfrac{\mathbf{P}\left((A\cap B)\cup(C\cap B)\right)}{\mathbf{P}(B)}\\ &=\dfrac{\mathbf{P}\left(A\cap B\right)+\mathbf{P}\left(C\cap B\right)}{\mathbf{P}(B)}\\ &=\mathbf{P}(A|B)+\mathbf{P}(C|B). \end{align}\]
The Multiplication Rule
From the definition of conditional probability, we have \(\mathbf{P}(A\cap B)=\mathbf{P}(A\lvert B)\,\mathbf{P}(B).\) Moreover, since \(\mathbf{P}(A\cap B)=\mathbf{P}(B\cap A)=\mathbf{P}(B\lvert A)\,\mathbf{P}(A)\), then
\[\mathbf{P}(A\cap B)=\mathbf{P}(A\lvert B)\,\mathbf{P}(B)=\mathbf{P}(B\lvert A)\,\mathbf{P}(A).\]Extending this to 3 sets, we have
\[\begin{align} \mathbf{P}(A\cap B\cap C)&=\mathbf{P}(A\cap B)\,\mathbf{P}(C\lvert A\cap B)\\ &=\mathbf{P}(A)\,\mathbf{P}(B\lvert A)\,\mathbf{P}(C\lvert A\cap B). \end{align}\]In general, for sets \(A_1,A_2,\ldots,A_n\),
\[\mathbf{P}(A_1\cap\ldots\cap A_n)=\mathbf{P}(A_1)\prod_{i=2}^{n}\mathbf{P}(A_i\lvert A_1\cap\ldots\cap A_{i-1}).\]Total Probability Theorem
Let’s partition our sample space \(\Omega\) into \(A_1, A2\) and \(A_3\), as shown in the figure below.
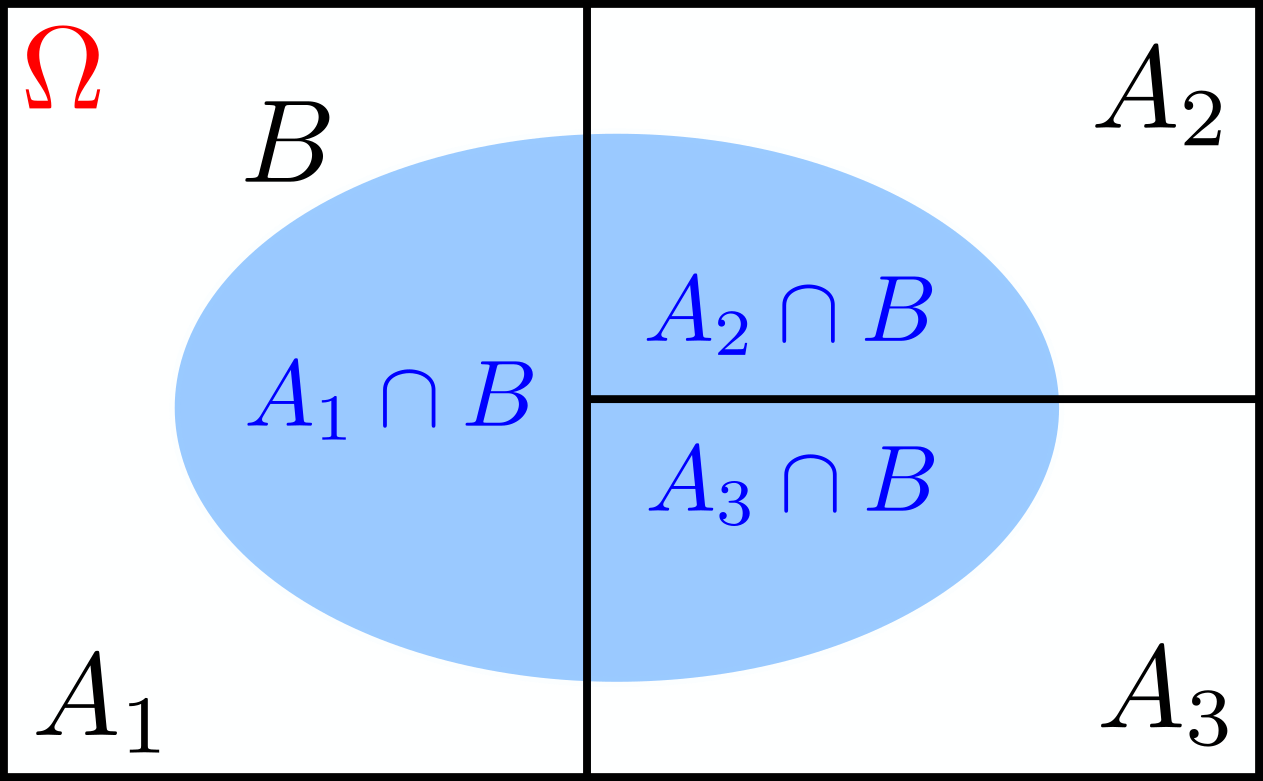
Then, for any set \(B\), we have
\[\begin{align} \mathbf{P}(B)&=\mathbf{P}(A_1\cap B)+\mathbf{P}(A_2\cap B)+\mathbf{P}(A_3\cap B)\\ &=\mathbf{P}(A_1)\,\mathbf{P}(B\lvert A_1)+\mathbf{P}(A_2)\,\mathbf{P}(B\lvert A_2)+\mathbf{P}(A_3)\,\mathbf{P}(B\lvert A_3). \end{align}\]In general,
\[\mathbf{P}(B)=\sum_{i}\mathbf{P}(A_i)\,\mathbf{P}(B\lvert A_i).\]