Basic Set Theory
A set is simply a collection of distinct elements. We usually denote a set by parentheses, \(\{\cdots\}\). It can have a finite number of elements or it can be infinite. It can also be countable or uncountable.
Empty and Universal Sets
A set that has no elements is called an empty set and we will denote it by \(\varnothing\). On the other hand, a set that contains everything is called universal set which we will denote by \(\Omega\).
Complement Set
The complement of a set \(A\), denoted by \(A^\mathsf{C}\), is the set of elements not belonging to \(A\) but are in the universal set. Mathematically,
\[A^\mathsf{C}=\{a\in\Omega: a\notin A\}.\]The complement of the universal set \(\Omega\) is the empty set \(\varnothing\), i.e., \(\Omega^\mathsf{C}=\varnothing\). Moreover, the complement of the complement of a set \(A\) is the set itself, i.e., \((A^\mathsf{C})^\mathsf{C}=A\). The figure below shows the complement of \(A\) as the shaded region.
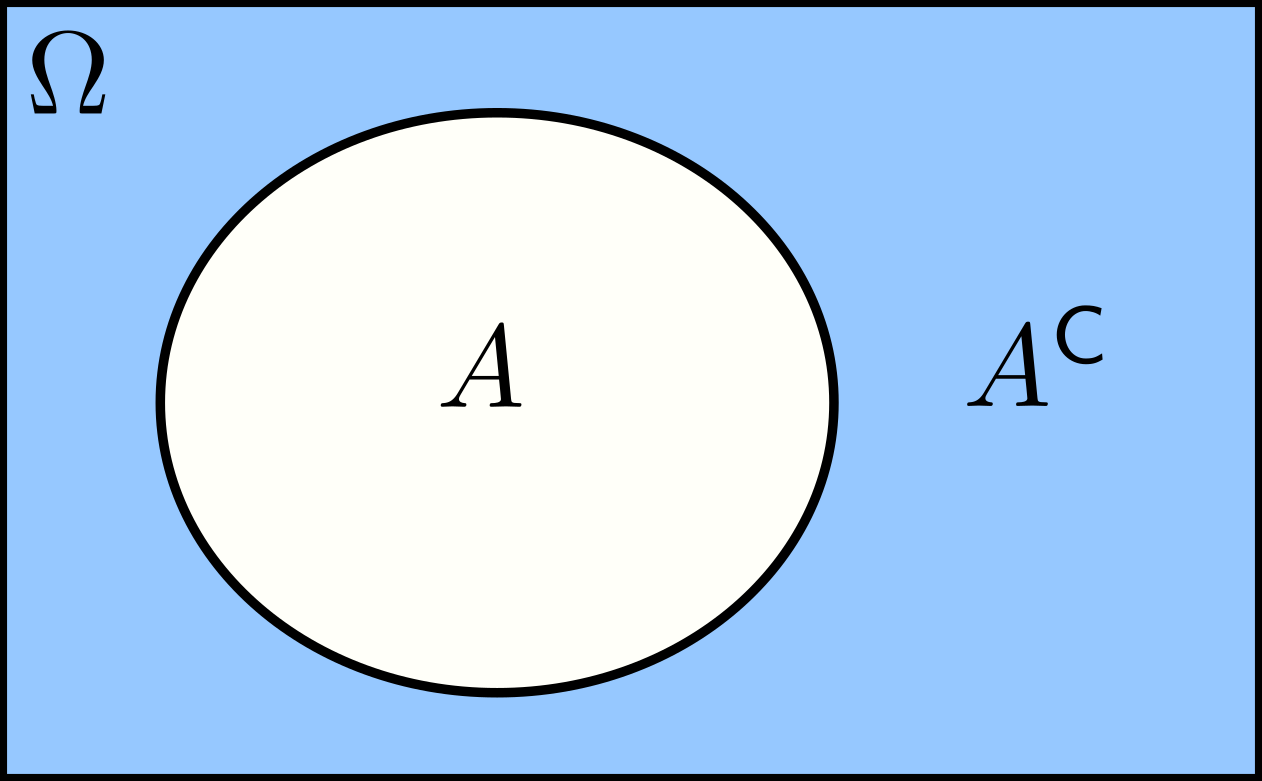
Union
The union of two sets, \(A\) and \(B\), is the set of elements that are in \(A\) or \(B\). We denote this by \(\cup\), i.e.,
\[A\cup B=\{c\in\Omega:c\in A\;\text{or}\;c\in B\}.\]The shaded region in the figure below shows the union of \(A\) and \(B\). Note that it includes elements that are in both \(A\) and \(B\).
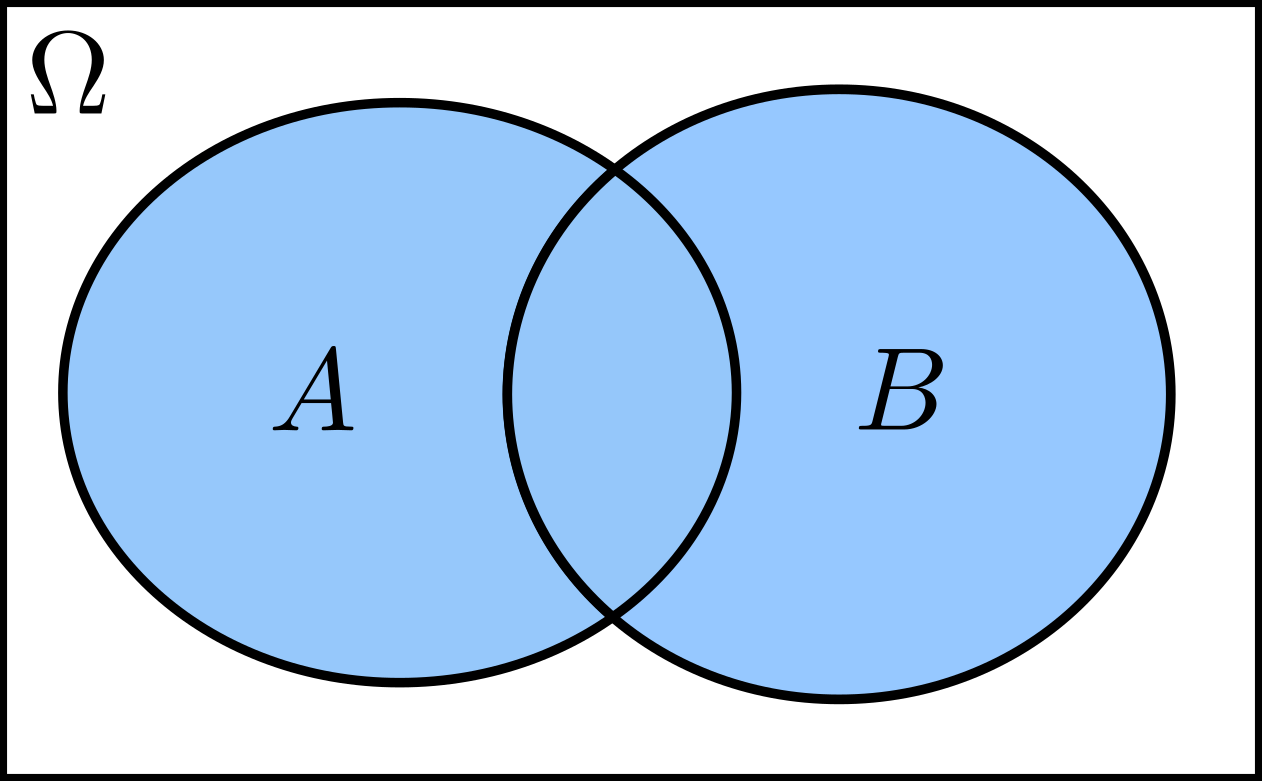
Intersection
The intersection of \(A\) and \(B\) is the set of elements that are in \(A\) and \(B\). We denote this with \(\cap\), i.e.,
\[A\cap B=\{c\in\Omega:c\in A\;\text{and}\;c\in B\}.\]The shaded region in the following figure shows the intersection of \(A\) and \(B\).
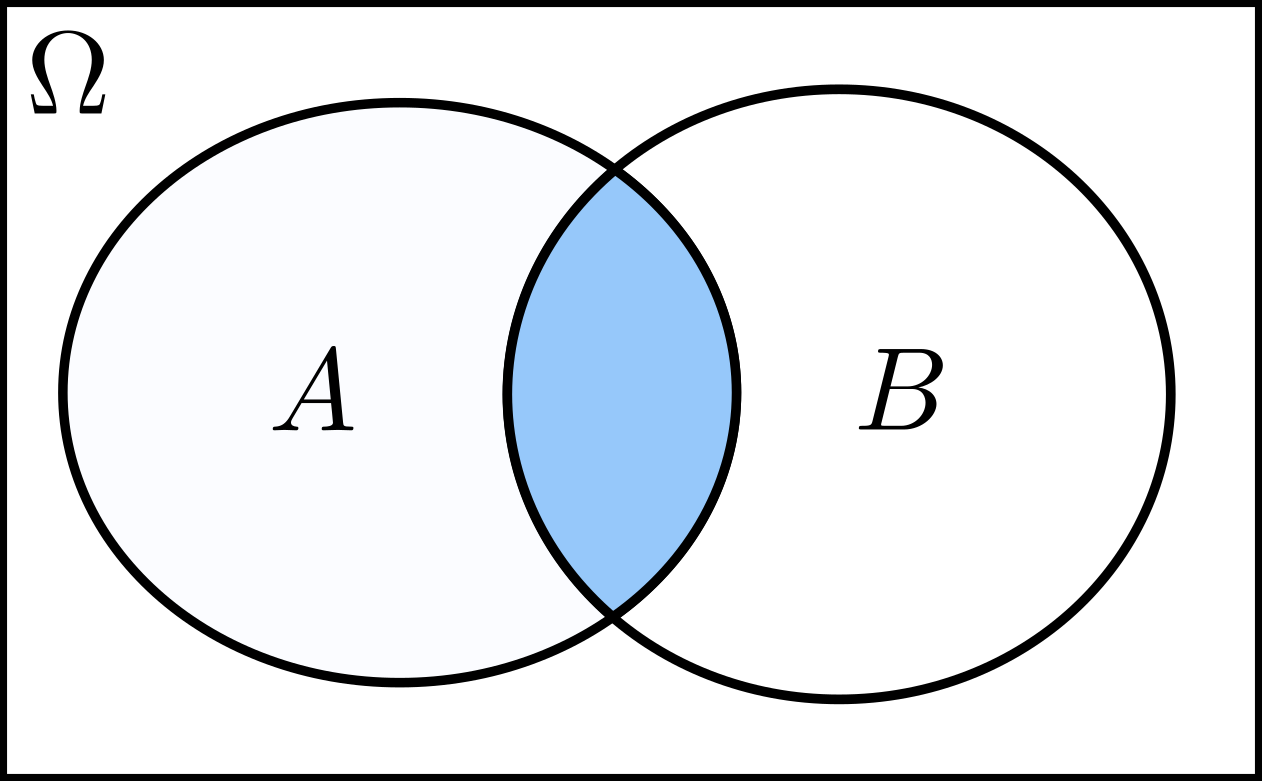
We say that two sets, \(A\) and \(B\), are disjoint or mutually exclusive whenever their intersection is the empty set, i.e., \(A\cap B=\varnothing\).
Set Properties
Here are a few interesting properties of sets.
| \(A\cup B=B\cup A\) | \(A\cap A^\mathsf{C}=\varnothing\) | |
| \(A\cup\Omega=\Omega\) | \(A\cap\Omega=A\) | |
| \(A\cap (B\cup C)=(A\cap B)\cup (A\cup C)\) | \(A\cup (B\cup C)=(A\cup B)\cup C\) |
de Morgan’s Laws
The first of de Morgan’s laws states that the complement of the union of sets is equal to the intersection of their complements:
\[\left(\bigcup_{n}S_n\right)^{\!\mathsf{C}}=\bigcap_{n}\left(S_n\right)^{\mathsf{C}}.\]The symbol \(\bigcup\) means we have to take the union of all the sets \(S_n\) while \(\bigcap\) means we have to take the intersection of all the sets. series: “ACME series” weight: 1.0 The second law states that the complement of the intersection of sets is equal to the union of their complements:
\[\left(\bigcap_{n}S_n\right)^{\!\mathsf{C}}=\bigcup_{n}\,(S_n)^\mathsf{C}.\]Sequences and their Limits
A sequence is an ordered collection of elements from a set \(S\). We can denote a sequence with \(a_i\) or \(\{a_i\}\) where \(i\) is a natural number, i.e., \(i\in\mathbb{N}\). We can also list the first few elements, e.g., \(a_1, a_2, a_3, \ldots\) The elements of a sequence does not have to be single numbers. They can be vectors, in which case we have a sequence of vectors. Formally, a sequence is a function \(f\) that takes an element from the set of natural numbers and associates with it an element of another set \(S\), i.e., \(f:\mathbb{N}\rightarrow S\).
Convergence of Sequences
We say that a sequence \(\{a_i\}\) converges if it approaches some limit \(a\). Formally,
\[\lim_{i\rightarrow\infty}a_i=a\]if, for any \(\epsilon>0\), there exists \(N\), such that if \(i>N\), then \(\lvert a_i-a\rvert<\epsilon\). To get an intuition about this statement, we visualize a convergent sequence in the plot below.
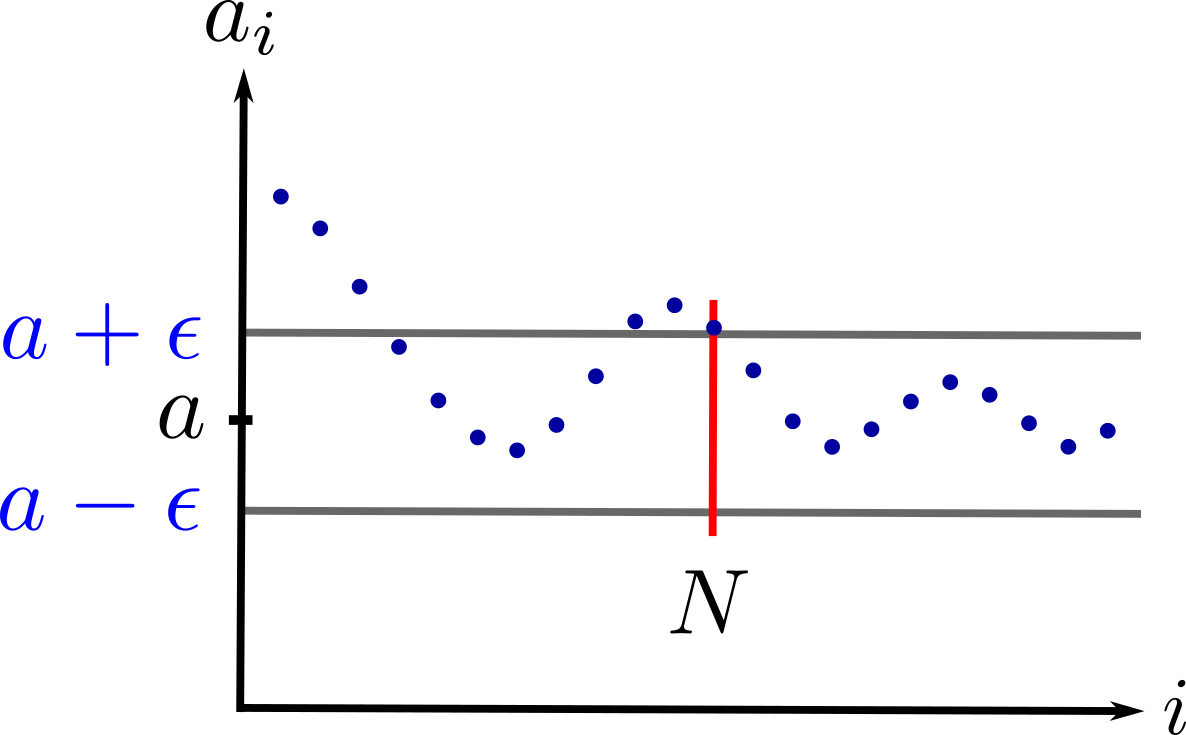
Notice how, after \(N\) terms, subsequent terms are confined inside the upper and lower bounds (gray lines). A sequence is convergent if this happens for any \(\epsilon\), no matter how small it is.
If the sequence does not converge, we say that it is divergent.
Properties
- If two sequences, \(a_i\) and \(b_i\), converge to \(a\) and \(b\), respectively, then:
- If \(g\) is a continuous function, then
Infinite Series
Given an infinite sequence \(\{a_i\}\), we add the first \(n\) terms to get a series. An infinite series is then the limit of this sum as \(n\) goes to infinity, i.e.,
\[\lim_{n\rightarrow\infty}\sum_{i=1}^{n}a_i=\sum_{i=1}^{\infty}a_i\]provided this limit exists.
Geometric Series
The geometric series is given by
\[S=\sum_{i=0}^{\infty}\alpha^i=1+\alpha+\alpha^2+\ldots\]This series will converge if \(\lvert\alpha\rvert<1\), in which case we have
\[S=\dfrac{1}{1-\alpha}.\]