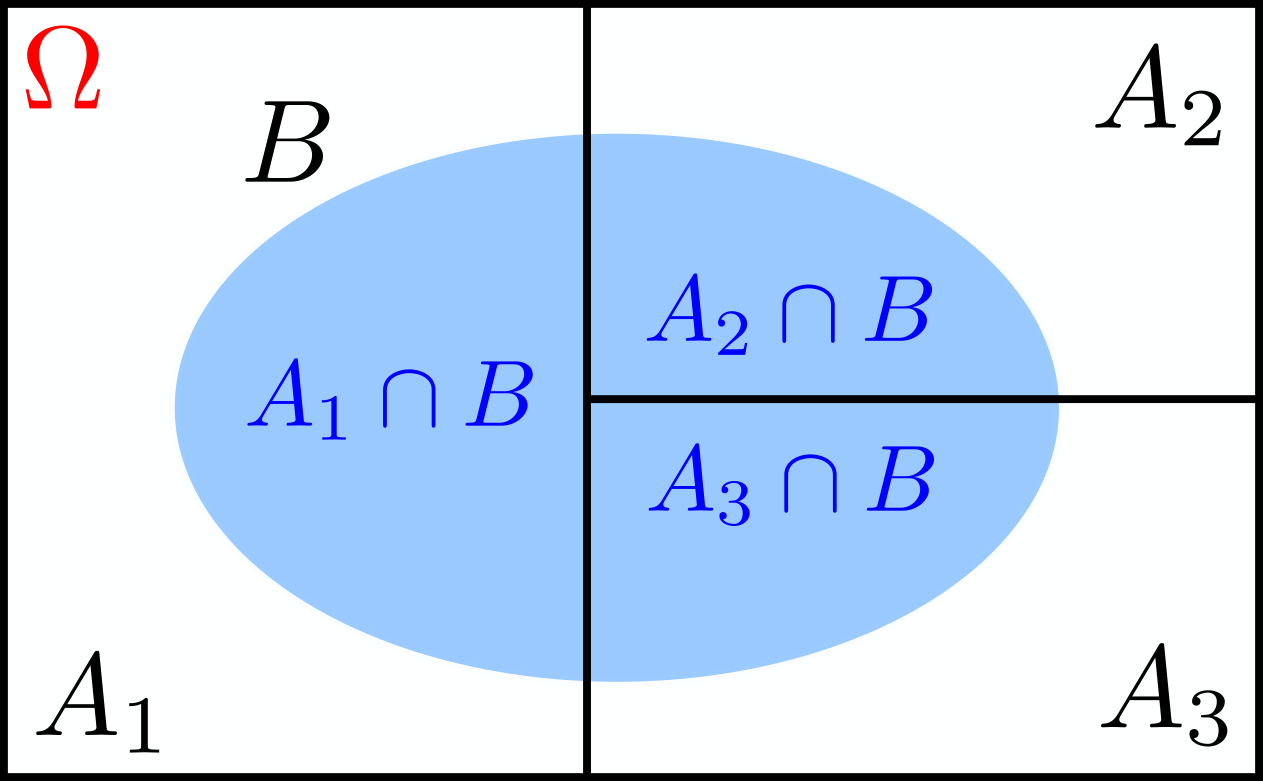
As with the discussion on the total probability theorem, we partition our sample space into \(A_1, A_2,\) and \(A_3\) as shown in the figure above. The probabilities \(\mathbf{P}(A_i)\) constitute our initial “beliefs” and they are called the prior probability of \(A\). Given that event \(B\) occurred, we now have to revise those “beliefs”. We have
\[\mathbf{P}(A_i\lvert B)=\dfrac{\mathbf{P}(A_i\cap B)}{\mathbf{P}(B)}=\dfrac{\mathbf{P}(A_i)\,\mathbf{P}(B\lvert A_i)}{\sum_{j}\mathbf{P}(A_j)\,\mathbf{P}(B\lvert A_j)}.\]The probabilities \(\mathbf{P}(A_i\lvert B)\) are called the posterior probability of \(A\).
Example
Consider a scenario where 5% of the population has covid. A particular covid test can detect the virus 90% of the time. However, it also shows false positives 9.5% of the time, i.e., it gives a positive result even if the person doesn’t have the virus. If Bob took the test and it gave a positive result, what is the probability that Bob has covid?
Let \(\mathbf{P}(C_{+})=0.05\) denote the probability that a person has covid. Also, let \(\mathbf{P}(T_{+}\lvert C_{+})=0.90\) denote the rate of true positives for the test and \(\mathbf{P}(T_{+}\lvert C_{-})=0.095\) the rate of false positives. Then,
\[\begin{align} \mathbf{P}(C_{+}\lvert T_{+})&=\dfrac{\mathbf{P}(C_{+})\,\mathbf{P}(T_{+}\lvert C_{+})}{\mathbf{P}(C_{+})\,\mathbf{P}(T_{+}\lvert C_{+})+\mathbf{P}(C_{-})\,\mathbf{P}(T_{+}\lvert C_{-})}\\ &=\dfrac{(0.05)(0.90)}{(0.05)(0.90)+(0.95)(0.095)}\\ &=0.3327 \end{align}\]There is a 33.27% chance that Bob has covid given that the test was positive.