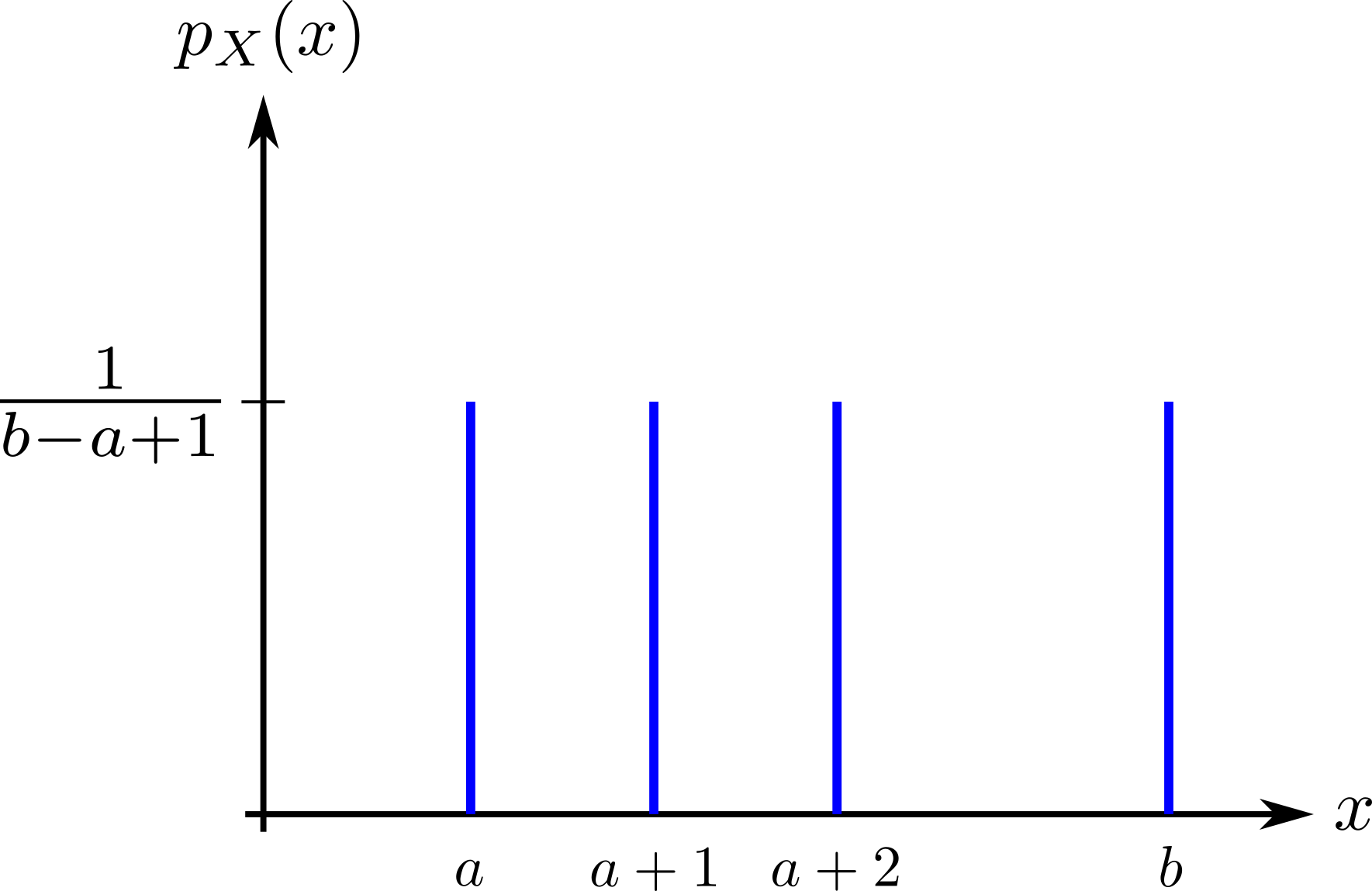
The sample space for a discrete uniform distribution is the set of integers from \(a\) to \(b\), i.e., its parameters are \(a\) and \(b\). We denote it by \(\mathrm{Unif}(a,b)\). All elements of the sample space have equal probability. Since there are \(b-a+1\) elements in the sample space, the PMF for a discrete uniform distribution is
\[p_X(x)=\dfrac{1}{b-a+1}.\]Expectation
The mean of a discrete uniform random variable is
\[\mathbb{E}[X]=\frac{a+b}{2}.\]$$\begin{align} \mathbb{E}[X]&=\frac{1}{b-a+1}\left(a+a+1+\ldots+b-1+b\right)\\ &=\frac{1}{b-a+1}\left(\frac{b-a+1}{2}\right)\left(a+b\right)\\ &=\frac{a+b}{2} \end{align}$$
Variance
The variance of a discrete uniform random variable is
\[\mathrm{var}(X)=\tfrac{1}{12}(b-a)(b-a+2).\]To calculate the variance, we have $$\begin{align} \mathrm{var}(X)&=\mathbb{E}[X^2]-(\mathbb{E}[X])^2\\ &=\frac{1}{b-a+1}\left[(a)^2+(a+1)^2+\ldots+(b)^2\right]-\left(\frac{a+b}{2}\right)^2. \end{align}$$ Before we proceed, we have to figure out the sum $$a^2+\ldots+b^2.$$ In the following, we will calculate the sum $$a^2+(a+1)^2+\ldots+b^2.$$ Recall from high school algebra that $$n^3-(n-1)^3=3n^2-3n+1.$$ Using this relation repeatedly, we have $$\begin{align} b^3-(b-1)^3&=3b^2-3b+1\\ (b-1)^3-(b-2)^3&=3(b-1)^2-3(b-1)+1\\ \vdots\qquad&=\qquad\vdots\\ a^3-(a-1)^3&=3a^2-3a+1. \end{align}$$ Summing both sides, we get $$b^3-(a-1)^3=3(a^2+\ldots+b^2)-3(a+\ldots+b)+(b-a+1).$$ Rearranging this equation gives $$\begin{align} a^2+\ldots+b^2&=\frac{1}{3}\left[b^3-(a-1)^3+3(a+\ldots+b)-(b-a+1)\right]\\ &=\frac{1}{3}\left[b^3-(a-1)^3+\frac{3}{2}(b-a+1)(a+b)-(b-a+1)\right]. \end{align}$$ Using the relation $$x^3-y^3=(x-y)(x^2+xy+y^2),$$ we get $$b^3-(a-1)^3=(b-a+1)\left[b^2+b(a-1)+(a-1)^2\right].$$ Consequently, $$\begin{align} a^2+\ldots+b^2&=\frac{b-a+1}{3}\left[b^2+b(a-1)+(a-1)^2+\frac{3}{2}(a+b)-1\right]\\ &=\frac{b-a+1}{3}\left[b^2+ab+a^2+\tfrac{1}{2}(b-a)\right]. \end{align}$$ Continuing our calculation of the variance, we have $$\begin{align} \mathrm{var}(X)&=\frac{1}{3}\left[b^2+ab+a^2+\tfrac{1}{2}(b-a)\right]-\frac{1}{4}(a+b)^2\\ &=\tfrac{1}{12}\left[4\!\left(b^2+ab+a^2\right)+2(b-a)-3(a+b)^2\right]\\ &=\tfrac{1}{12}\left[\left(b^2-2ab+a^2\right)+2(b-a)\right]\\ &=\tfrac{1}{12}(b-a)(b-a+2). \end{align}$$