Consider a trial where there are only two possible outcomes: success/failure, head/tail, etc. To model this experiment, we use a Bernoulli random variable denoted by \(\mathrm{Ber}(p)\). A Bernoulli random variable \(X\) takes on the value \(1\) with probability \(p\) or \(0\) with probability \(1-p\), i.e.,
\[X=\begin{cases} 1, & \text{with probability}\quad p\\ 0, & \text{with probability}\quad 1-p. \end{cases}\]We can write the PMF of a Bernoulli random variable as
\[p_X(x)=p^x(1-p)^{1-x}.\]Expectation and Variance
The expectation of a Bernoulli random variable is
\[\begin{align} \mathbb{E}[X]&=\sum_{x}xp_X(x)\\ &=1\cdot(p)+0\cdot(1-p)\\ &=p \end{align}\]Its variance is
\[\begin{align} \mathrm{var}(X)&=\mathbb{E}[(X-\mathbb{E}[X])^2]\\ &=(1-p)^2\cdot p+(0-p)^2\cdot(1-p)\\ &=p(1-p)(1-p+p)\\ &=p(1-p) \end{align}\]Indicator Random Variable
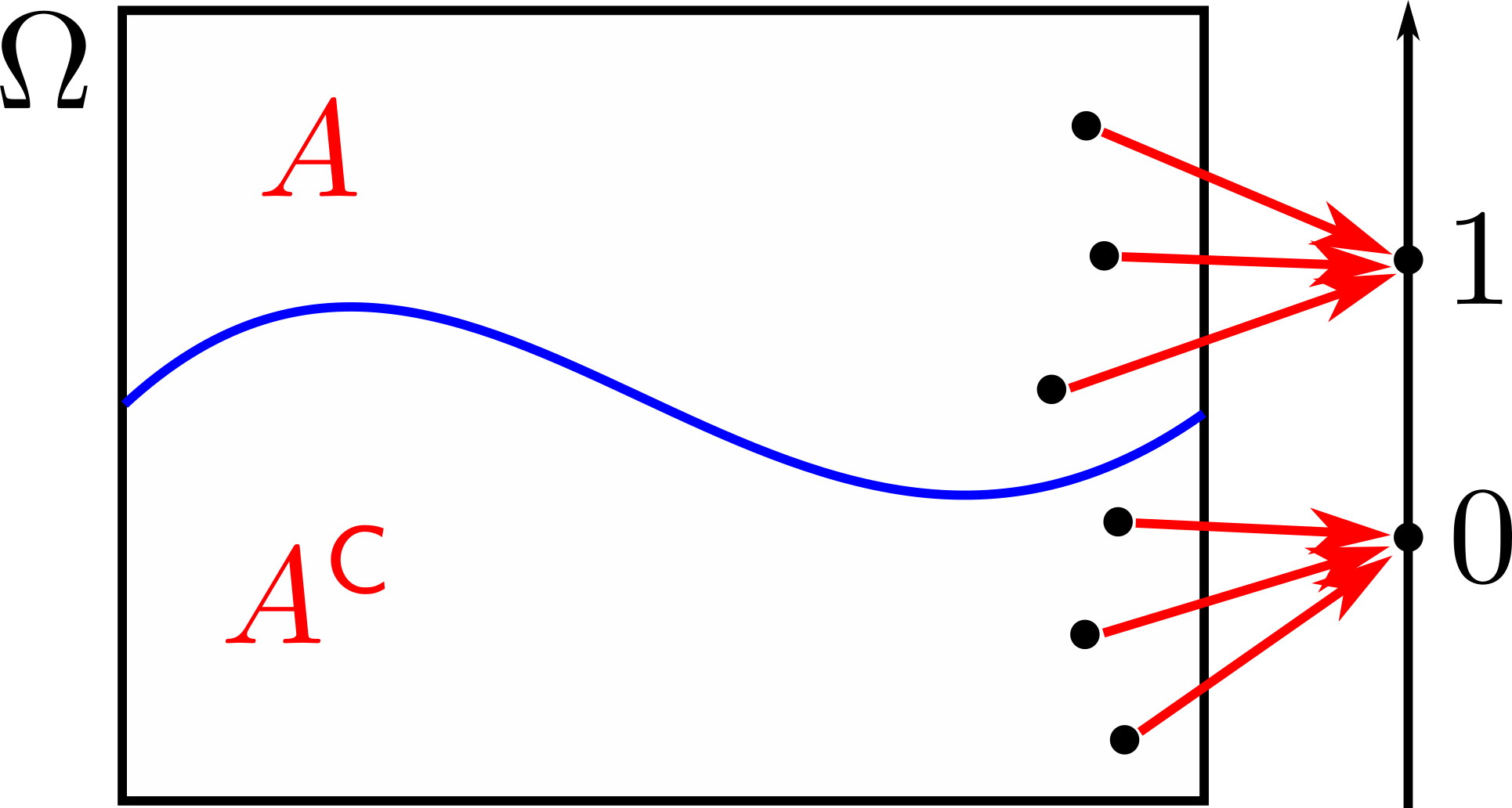
The indicator random variable \(I_A\) takes on the value \(1\) if and only if the event \(A\) occurs. Otherwise, it’s \(0\). Given that the probability of event \(A\) occurring is \(\mathbf{P}(A)\), then the expectation of an indicator random variable is
\[\begin{align} \mathbb{E}[I_A]&=1\cdot\mathbf{P}(A)+0\cdot\mathbf{P}(A^\mathsf{C})\\ &=\mathbf{P}(A). \end{align}\]