Suppose we have to choose 10 items from a bowl that contains 1000 items. In how many ways can we do this? That is, how many possible outcomes are there? If the bowl contains 300 red and 700 blue items, what is the probability that we will get 10 blue items? In many models, calculating probabilities reduces to counting the number of elements of a given set.

Multiplication Principle

If an experiment has \(r\) stages and there are \(n_i\) possibilities for each stage \(i\), then the total number of possibilities is \(n_1\cdot n_2\cdots n_r.\) For example, if there are 5 shirts, 4 jackets, and 3 pants, then the total number of possible attires is \(5\cdot 4\cdot 3=60\).

Permutation

Consider a set \(A\) with \(n\) elements, \(A=\{a_1,\ldots,a_n\}.\) A permutation of \(A\) is an ordered arrangement of its elements. How many possible arrangements are there? Since there are \(n\) items, we can put all of them in \(n\) boxes. For the first box, we have \(n\) choices. For the second box, we are left with \(n-1\) choices. For the third box, there are \(n-2\). We proceed this way until we’ve put the last item in a box.

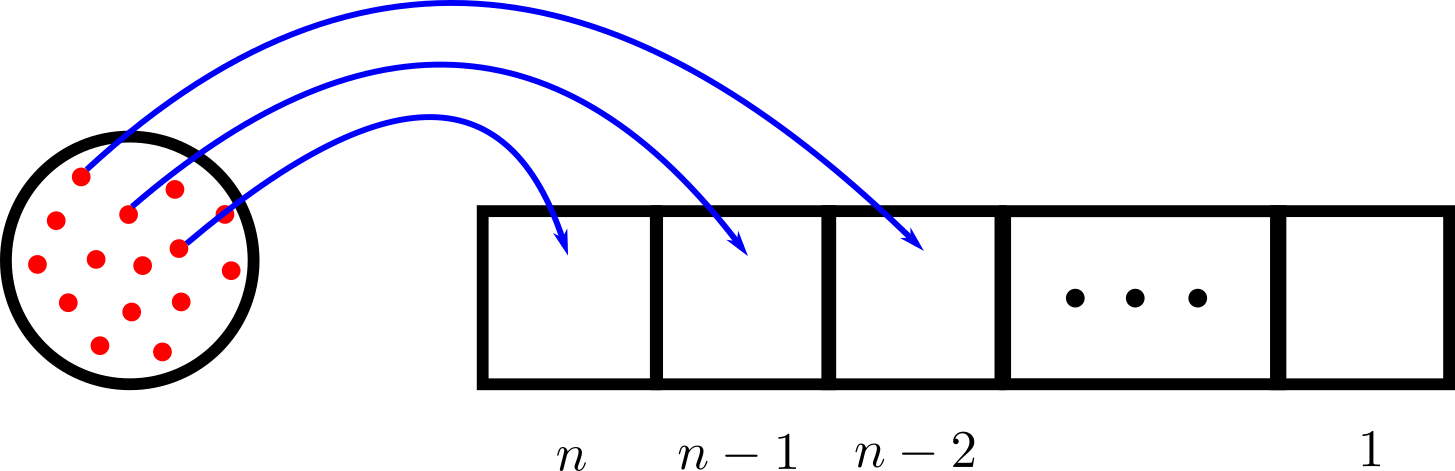
Using the multiplication principle, we have

\[n\cdot(n-1)\cdot(n-2)\cdots 2\cdot 1=n!\]

arrangements. The symbol \(!\) is called a factorial and \(n!\) is read as “\(n\) factorial.” If there were 5 items, then the number of permutations is

\[5!=5\cdot4\cdot3\cdot2\cdot1=120.\]

Suppose now that, instead of using all the items in \(A\), we have to select \(r\) items. In how many ways can we do this? It depends on whether we can duplicate the items or not. If we can duplicate the items, then we are sampling with replacement. Otherwise, we are sampling without replacement.

  • Sampling With Replacement

    If we are sampling with replacement, we put the items back before picking the next item. There will be a chance of picking the same item again. The number of ways of picking \(r\) items from \(n\) elements is

    \[n^r.\]

  • Sampling Without Replacement

    If we are sampling without replacement, there is no chance of picking the same item again. The number of ways of picking \(r\) items is

    \[n\cdot(n-1)\cdot(n-2)\cdots(n-r+1)=\dfrac{n!}{(n-r)!}.\]

    We also denote this by \({}_nP_r\).

Combination

Suppose we now pick \(r\) items from \(A\), disregarding their order. In how many ways can this be done? We can do this in two steps. First, we pick \(r\) items from \(A\) and the number of ways to do this is

\[\dfrac{n!}{(n-r)!}.\]

Next, we know there are \(r!\) ways to order the items. Therefore, if we disregard their order, there are

\[\dfrac{n!}{r!(n-r)!}=\binom{n}{r}\]

possible combinations where \(\binom{n}{r}\) is called the binomial coefficient. This is also denoted by \({}_nC_r\). We can interpret the binomial coefficient as the number of \(r\)-element subsets of a set with \(n\) elements.

Number of Subsets

If a set \(A\) has \(n\) elements, how many possible subsets are there? First, the empty set is a subset of \(A\) and we denote this by \(\binom{n}{0}\). If we consider subsets with a single element, then there are \(\binom{n}{1}=n\) subsets. Continuing this process, the number of subsets is

\[\sum_{k}^{n}\binom{n}{k}=\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{n}=2^n.\]