Definition
Intuitively, we would say that two events \(A\) and \(B\) are independent if knowing that one event occurred gives us no information about the other event. We can put this into mathematical form by stating that \(\mathbf{P}(B\lvert A)=\mathbf{P}(B)\) or \(\mathbf{P}(A\lvert B)=\mathbf{P}(A)\). From this, we say that events \(A\) and \(B\) are independent if
\[\mathbf{P}(A\cap B)=\mathbf{P}(A)\,\mathbf{P}(B).\]Disjoint Events
Disjoint events are not necessarily independent. Consider the figure below.
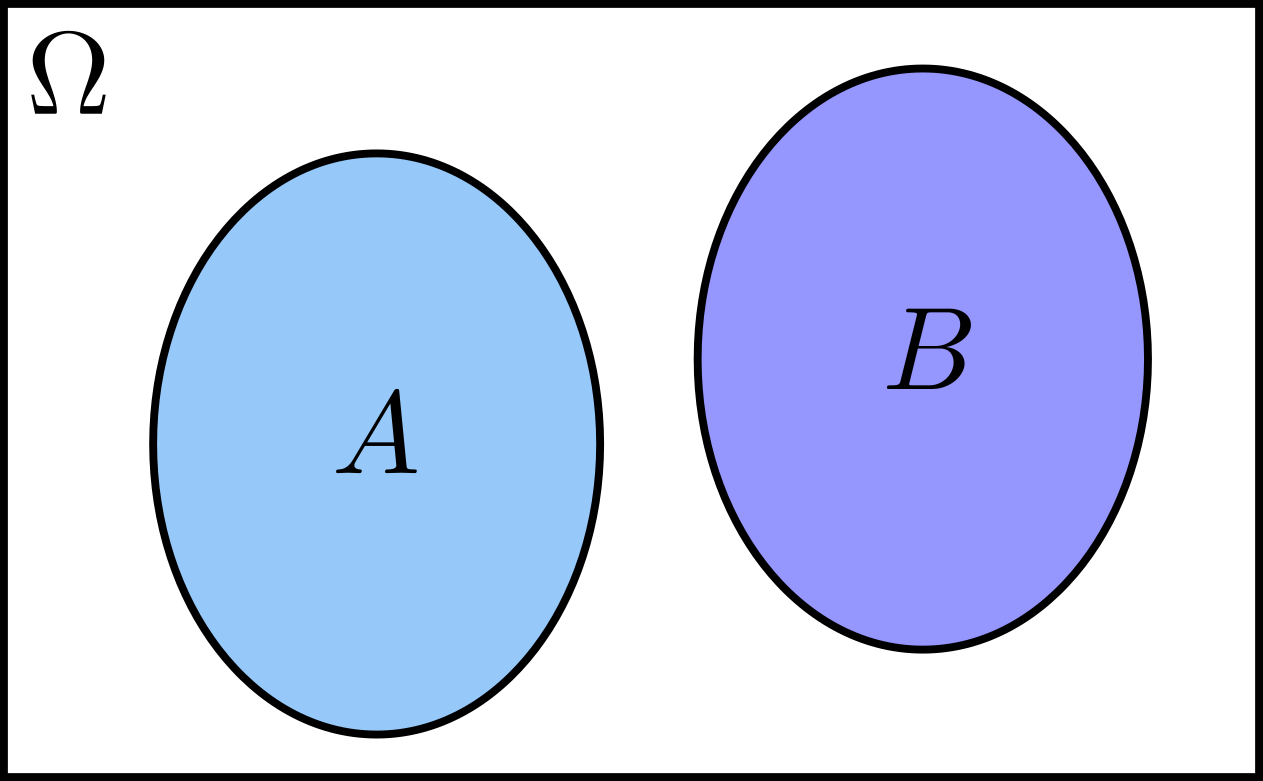
We have \(\mathbf{P}(A)>0\), \(\mathbf{P}(B)>0\) and \(\mathbf{P}(A\cap B)=0\) so that
\[\mathbf{P}(A\cap B)\neq\mathbf{P}(A)\,\mathbf{P}(B).\]\(A\) and \(B\) are not independent.
Independence of Complements
If \(A\) and \(B\) are independent, then \(A\) and \(B^\mathsf{C}\) are independent.
Conditional Independence
Two events, \(A\) and \(B\), are conditionally independent if, given that event \(C\) occurred,
\[\mathbf{P}(A\cap B\lvert C)=\mathbf{P}(A\lvert C)\,\mathbf{P}(B\lvert C).\]Now, assume that \(A\) and \(B\) are independent. Are they conditionally independent if \(C\) occurred? No.
Mutual Independence
We now generalize the idea of independence to a collection of events. We say that events \(A_1, A_2,\ldots,A_n\) are mutually independent if
\[\mathbf{P}(A_i\cap A_j\cap\cdots\cap A_m)=\mathbf{P}(A_i)\,\mathbf{P}(A_j)\ldots\mathbf{P}(A_m)\]for any distinct indices \(i,j,\ldots,m\).